-
Eurocode 1 appliqué aux bâtiments de forme complexe
-
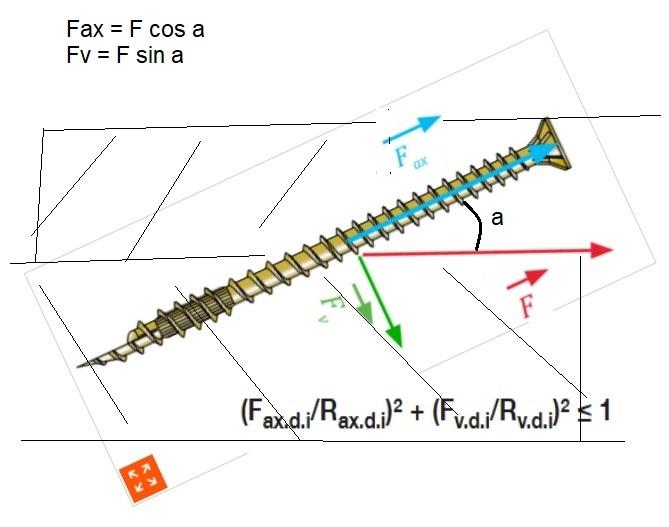
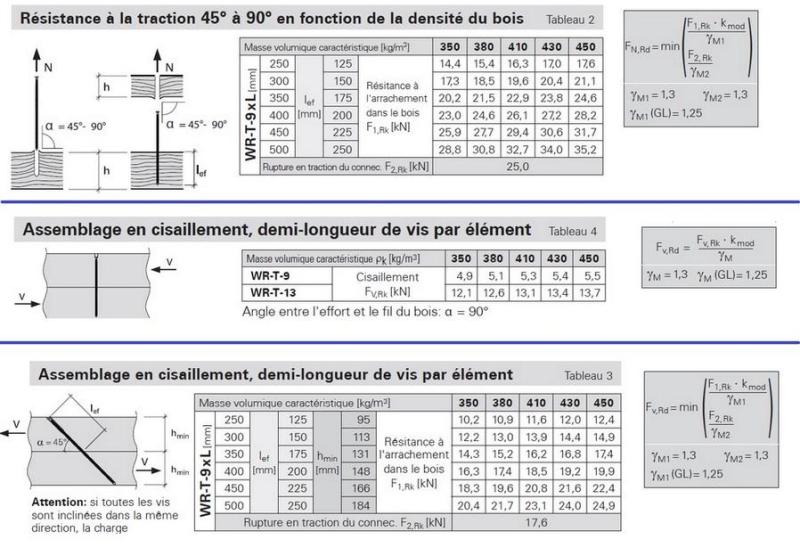
Vis structurelles bois dispensées de sollicitation au cisaillement ??
-
Vis structurelles bois dispensées de sollicitation au cisaillement ??
-
Vis structurelles bois dispensées de sollicitation au cisaillement ??
-
Vis structurelles bois dispensées de sollicitation au cisaillement ??
-
Cadres dans une poutre sur la longueur de l'appui
-
Cadres dans une poutre sur la longueur de l'appui
-
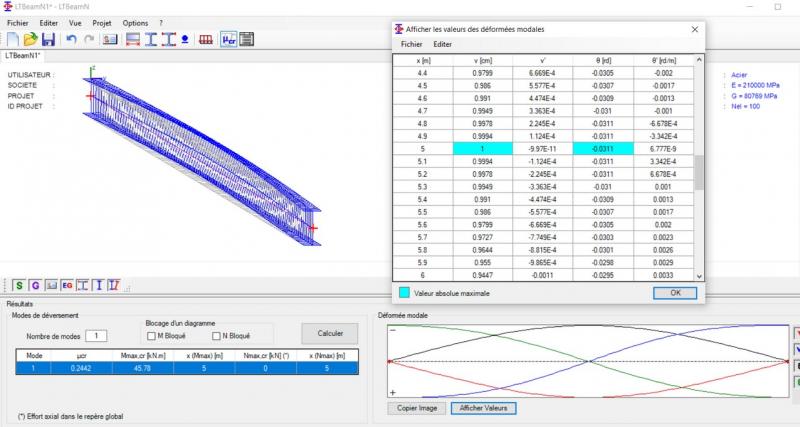
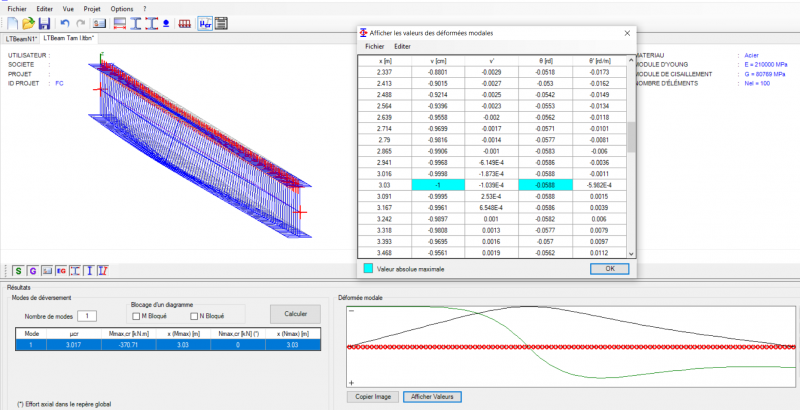
Evaluation des déformations de déversement dans LTbeam
-
Evaluation des déformations de déversement dans LTbeam
-
Evaluation des déformations de déversement dans LTbeam
-
Evaluation des déformations de déversement dans LTbeam
-
Evaluation des déformations de déversement dans LTbeam
-
Evaluation des déformations de déversement dans LTbeam
-
Evaluation des déformations de déversement dans LTbeam
-
Evaluation des déformations de déversement dans LTbeam
Jean-Louis François
Membres
-
Inscription
-
Dernière visite







.jpg.3ecf74647c0e7004bf94c362a9848bef.jpg)