- Réponses 12
- Vues 4.5k
- Créé
- Dernière réponse
Meilleurs contributeurs dans ce sujet
-
 Hardy Cross 5 messages
Hardy Cross 5 messages -
 TOUATI Mohamed 3 messages
TOUATI Mohamed 3 messages -
 Bisudi Bazola Aimé 2 messages
Bisudi Bazola Aimé 2 messages -
 MEULAJE 1 message
MEULAJE 1 message
Jours populaires
Messages populaires
-
b et h sont toujours les dimensions de la section transversale.h n'est pas la hauteur.L'inertie est toujours liée à une section plane.
-
Bonsoir Mr HPAL, cette notion est definis par rapport à la section transversale de l'élement, donc pour un pôteau ou poutre rectangulaire la section tranversale se note par rapport aux dimension tra
-
Je vous remercie tous pour ces informations j'ai bien compris maintenant. Bonne soirée






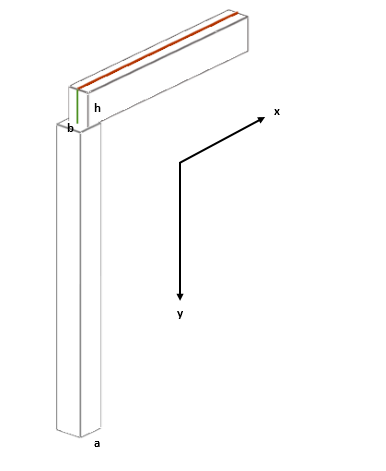
comment_109305Bonjour, svp j'arrive pas a comprende inertie suivant x, y et z ?
ca veut dire quoi physiquement ?
je sais que dans une poutre de dimensions (b,h) on a I = b*h^3 / 12 (d'apres le double intégrale)
mais dans x et y il y a l'introduction de la longueur du poutre
par exemple inertie suivant x = L * b^3 / 12 ????
rien pigé