- Réponses 17
- Vues 13.8k
- Créé
- Dernière réponse
Meilleurs contributeurs dans ce sujet
-
 Hicham Chabbouba 7 messages
Hicham Chabbouba 7 messages -
 ucefelmir 5 messages
ucefelmir 5 messages -
FRIDJALI 3 messages
-
 scorpion 2 messages
scorpion 2 messages
Jours populaires
Messages populaires
-
L'effort est vertical(effort tranchant ramené par la poutre), cet effort sera transmis au poteau sous deux composantes, l'une est un effort normal centré, l'autre sera un effort tranchant, principe de
-
bonjour, Désolé mais je pense que beaucoup de camarades devraient réviser les relations métriques dans le triangle et revoir la trigonométrie. A+
-
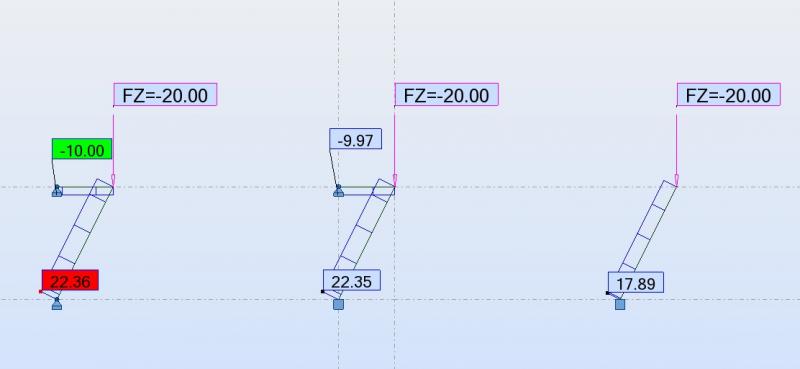
Bonjour, Avant de jeter un œil sur votre modèle, je vous invite à mener une réflexion sur les différents cas possibles : - Cas 1 : Poteau articulé à la base et attaché à un élément horizonta




comment_119732Bonjour,
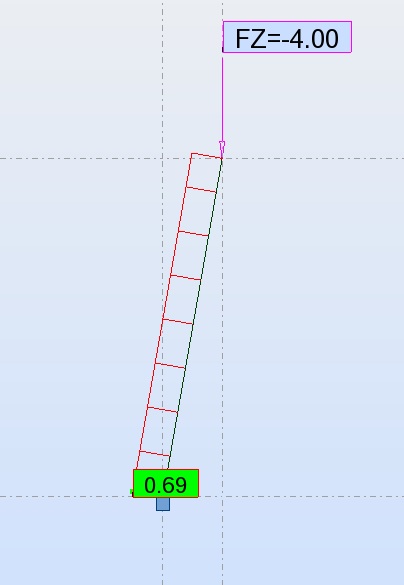
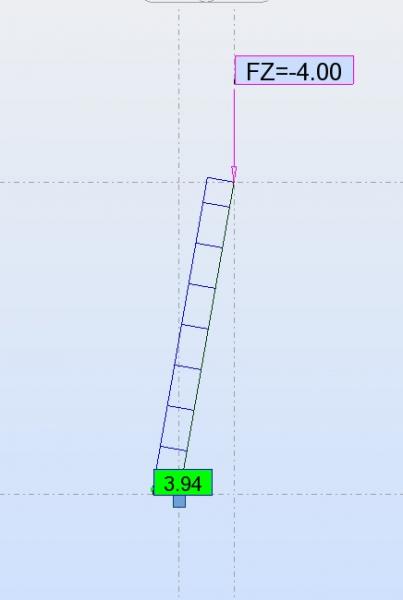
Je suis entrain d’étudier une simple structure un RDC avec des poteaux inclinés (voir fichier joint), je l'ai modélisé dans robot (version 2009) j'ai obtenu des résultats trop différents en cas de calcul manuel. Merci de me signaler où se trouve l'erreur.
L'inclinaison par rapport au vertical est 10 degre la hauteur de la structure est 4m, les charges G=0.36T et Q= 0.1T
Le calcul manuel:
l'effort a la tête du poteau est F=4T
N=F/cos10 =4.06 T
T=F/sin10=23.05 T
M= T*H=92T.m
Cordialement.