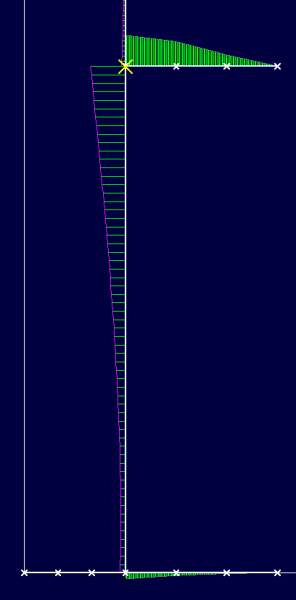
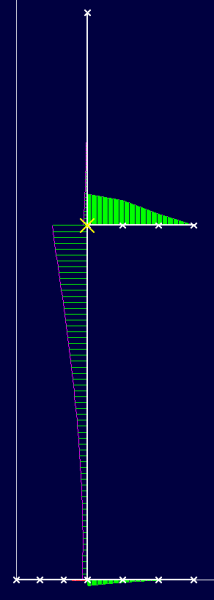
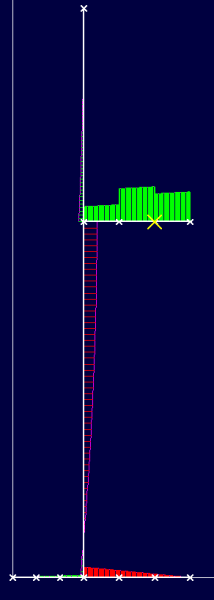
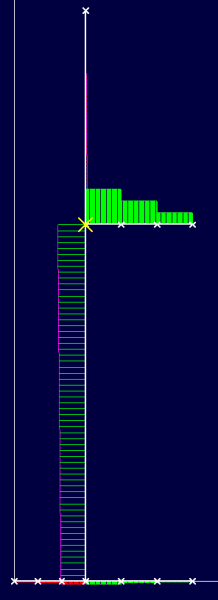
Senbleh Posted March 12, 2018 Report Share Posted March 12, 2018 Bonjour, je cherche la formule et la méthode de calcul d'une poutre console de section 20X40 et de 2,86m de portée avec un charge concentrée de G=1,20t et Q=0.1t. La poutre est encastrée d'un cote et libre sur l'autre. Merci pour vos éclairages. Quote Link to comment Share on other sites More sharing options...
DJARIRI Posted March 12, 2018 Report Share Posted March 12, 2018 1 Quote Link to comment Share on other sites More sharing options...
Rood Similien Posted March 13, 2018 Report Share Posted March 13, 2018 Quote Link to comment Share on other sites More sharing options...
Ahmed أحمد Posted March 13, 2018 Report Share Posted March 13, 2018 (edited) Edited March 13, 2018 by Ahmed Diagne Quote Link to comment Share on other sites More sharing options...
Senbleh Posted March 14, 2018 Author Report Share Posted March 14, 2018 Quote Link to comment Share on other sites More sharing options...
Ahmed أحمد Posted March 14, 2018 Report Share Posted March 14, 2018 (edited) Edited March 14, 2018 by Ahmed Diagne 1 Quote Link to comment Share on other sites More sharing options...
Walid Salmi Posted March 17, 2018 Report Share Posted March 17, 2018 Quote Link to comment Share on other sites More sharing options...
Expert philkakou Posted March 20, 2018 Expert Report Share Posted March 20, 2018 Quote Link to comment Share on other sites More sharing options...
gerard demeusy Posted March 24, 2018 Report Share Posted March 24, 2018 Quote Link to comment Share on other sites More sharing options...
vie en rose Posted March 30, 2018 Report Share Posted March 30, 2018 Quote Link to comment Share on other sites More sharing options...
Recommended Posts
Join the conversation
You can post now and register later. If you have an account, sign in now to post with your account.
Note: Your post will require moderator approval before it will be visible.