- Réponses 16
- Vues 10.9k
- Créé
- Dernière réponse
Meilleurs contributeurs dans ce sujet
-
hrhrh 8 messages
-
BELLAMINE 3 messages
-
breton2250 2 messages
-
 MAKER 1 message
MAKER 1 message
Jours populaires
Messages populaires
-
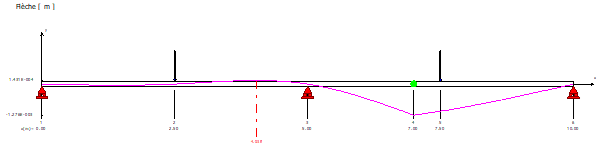
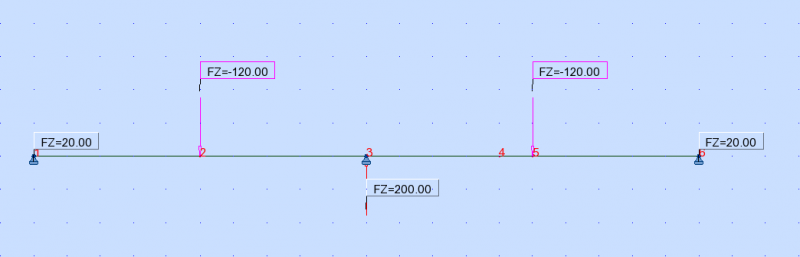
Bonjour La réaction d'appuis au point D ne peut être modélisée en appuis simple mais plutôt sur un appuis élastique de rigidité KD de tel sorte que RD=VD/KD VD : la flèche au point D. Et KD peut




comment_129945