- Réponses 18
- Vues 9.1k
- Créé
- Dernière réponse
Meilleurs contributeurs dans ce sujet
Jours populaires
Messages populaires
-
Bonjour, pas de réponse ? J'ai relu les messages d'Oliver qui s'avère être un petit cachotier car il ne nous dit pas tout !!!! (mais si mais si Mdr) S'il nous soumet la 4e question, c'est q
-
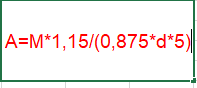
Pour t'aider un peu... En page 23 du document que j'ai fait sur la méthode de clapeyron sur les ouvrages à 3 travées, tu as la démarche analytique pour le calcul des réactions d'appui et des mome




comment_130694Bonjour tout le monde,
vous pouvez me dire comment je dois procéder pour résoudre cette exercice.
Merci d'avance pour votre aide.
Voici l'énoncé :
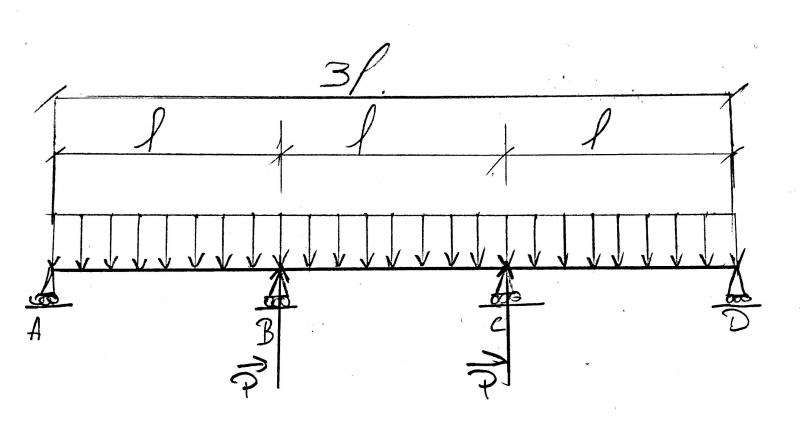
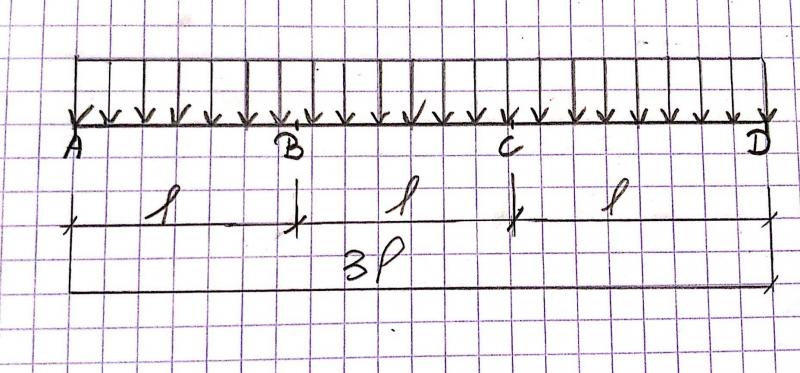
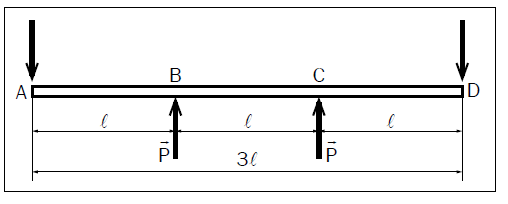
On considère une poutre AD reposant sur deux appuis simples A et D.
Sa longueur est L = 3l. Elle supporte une charge uniformément répartie d’intensité p (kN) par mètre linéaire.
Les questions :
4.a) Calculez les réactions d’appui en A et B sous la charge répartie d’intensité p.
4.b) Déduisez-en la valeur du moment fléchissant dans
les différents tronçons : AB, BC et CD. Tracez, avec précision, la ligne représentative correspondante. On donnera notamment les abscisses des moments maxi-mums dans chaque tronçon.
4.c) Montrez que l’expression du moment fléchissant
dans les trois tronçons peut se mettre sous la forme
M(x) =m(x)+M(1-x/l)+M x/l
où m(x) est l’expression du moment de la travée indépendante supportant les mêmes charges.
4.d) Vérifiez la relation de Clapeyron :
M(a) l + 4 M(b) l + M(c) l = - pl³/2
4.e) Montrez que l’on a également :
M(b) l + 4M(c) L + M(d) l = - pl³/2