Bonjour à tous,

Dimanche pluvieux, 12 degrés, un fort ennuis alors je poste 

La justification des voiles par passes est souvent négligée dans les rapports des géotechniciens, laissant ainsi seul le structuraliste ou l'entreprise pour justifier notamment les massifs au pied des butons (cela rejoint la discussion lancée par @Bellamine).

Je vous propose ici un petit utilitaire appelé "KaMEL" qui comme son nom l'indique utilise le coefficient de poussée des terres (Ka) et la Méthode d'Equilibre Limite (MEL) pour étudier rapidement les efforts dans un voile, les butons et le massif.

2 petites précautions avant :

• ce petit utilitaire que vous pouvez utiliser gratuitement sur le site lelabgeolpack.com, dans la rubrique "utilitaires" accessible sur le menu de gauche DOIT être utilisé uniquement en avant-projet. Pour les phases PRO ou EXE je vous conseille fortement d'utiliser une approche MISS
• les équations de la statique ne permettent pas d'évaluer les déplacements. Par ailleurs, ces équations ne tenant pas compte de la rigidité des éléments, elles ont tendance à sous estimer (ou sur estimer) les moments par rapport à un vrai calcul MISS. 

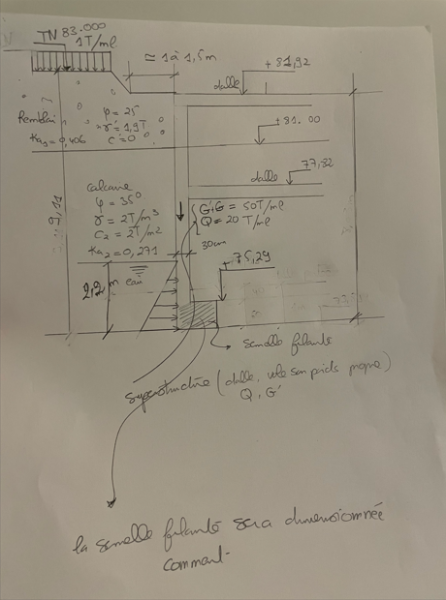
Ceci étant dit, prenons un exemple que l'on retrouve souvent sur de nombreux documents disponibles sur internet. On propose de considérer ici le cas d'un projet de construction d'un bâtiment sur 2 niveaux de sous-sols. Les terrassements sont prévus entièrement en voiles de béton projeté mis en œuvre par bandeaux et par passes alternées, butonnés sur 6.25 mètres de hauteur !

On suppose un limon sableux avec les caractéristiques suivantes :

A court terme, en considérant les caractéristiques non drainées, les terrassements vont pouvoir se faire par bandeaux de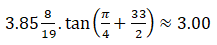 mètres de hauteur (déduction faites de l'abaque de Taylor-Biarez) sur laquelle on va appliquer un coef. de sécurité de 1.50 soit des bandeaux de 2.00 mètres de hauteur environ.

Au fur et à mesure de la réalisation des bandeaux, on va mettre en place des butons qui seront repris sur des massifs. Je ne peux pas détailler ici toutes les étapes mais à la fin on aura quelque chose ressemblant à ça :

Sur cette image, une 1ere rangée de buton s'écartant de 40° du voile, est mise en place à 4.65 m de hauteur, et une seconde rangée à 1.15 m de hauteur. Pour limiter l'inclinaison du massif au pied des butons, la première rangée de butons devra s'écarter du voile avec un angle si possible inférieur à 45°.

Sur 6.25 m de hauteur, en considérant les caractéristiques effectives des limons (phy' = 33° et C' = 0), la poussée des terres est alors de Ka.y.H => avec Ka = tan²(pi/4 - phy/2) = 0.295 => 0.295 x 19 x 6.25 = 35 kN/ml.

Notre calcul étant un calcul MEL, on appliquera un coef. de 1.35 aux actions permanentes et 1.50 aux actions variables. Soit une poussée des terres de 35 x 1.35 = 47.25 kN/ml. La distribution étant triangulaire, elle s'applique ici au tiers de la hauteur (2.083 mètres) et la poussée totale des terres est de 47.26 x 6.25 / 2 = 147.69 kN/ml.

On peut également envisager la présence d'une surcharge infinie en tête de voile, il vient alors pour une surcharge de 20 kPa :

Une poussée pondérée par 1.50 de 55.28 kN/ml appliquée à mi-hauteur (3.13 m).

On pourrait également avoir un bâtiment existant avec des semelles filantes proches du voile :

Ici par exemple, une semelle enterrée de 1.00 mètre (cote 5.25) de 1 mètre de large chargée à 8 T/ml...etc...l'utilitaire permet plusieurs cas de figure.

Nous retiendrons ici une surcharge infinie de 20 kPa en surface à l'arrière du voile. En assimilant le voile à une poutre sur 3 appuis simples (le pied du voile et les 2 butons), les équations de la statique nous donnent 3 équations d'équilibre : en translation ΣFx = 0 et ΣFy = 0 et en rotation ΣMz = 0.

ETAPE 1 : REACTIONS AU NIVEAU DES BUTONS

On peut schématiser notre voile comme ci-dessous :

Aux points A et B, la somme des moments est nulle, soit en A :

Et la somme des efforts appliqués selon y sur la poutre est nulle, soit :

Il est donc très simple d'isoler R1 dans la première formule, et de le substituer dans la seconde formule pour trouver facilement la valeur numérique de R2, puis celle de R1. Si on veut, on peut aussi isoler les actions :

 

En considérant des butons espacés de 2.50 mètres, il vient :

- dans les butons fixés à 4.65 mètres de hauteur : R = 39.38 + 31.19 = 70.57 x 2.50 = 176.44 kN

- dans les butons fixés à 1.15 mètre de hauteur : R = 108.30 + 24.08 = 132.38 x 2.50 = 330.97 kN

En considérant les inclinaisons des butons il vient :

- dans les butons fixés à 4.65 mètres de hauteur : 176.44 / sin(90°-40°) = 230.32 kN - la longueur du buton est de 6.74 mètres à laquelle on ajoutera 20 cm pour permettre de s'adapter en phase chantier...pour des butons de type tubes acier de 20 cm de diamètre, vous pouvez alors vérifier le tube selon l'EC3 avec l'utilitaire "TubeAcier" également disponible gratuitement sur le site lelabgeolpack.com 

- dans les butons fixés à 1.15 mètre de hauteur : 330.97 / cos (90°-70°) = 352.21 kN - avec une longueur de 4.94 mètres à laquelle on ajoutera 20 cm pour adaptation sur chantier.

Soit :

 

ETAPE 2 : JUSTIFICATION DU MASSIF

On suppose que des essais pressiométriques réalisés avant le démarrage du chantier ont permis d'obtenir une Ple* au niveau de l'assise du massif de l'ordre de 1000 kPa. On retiendra également Kp = 0.80 (cas défavorable). Pour bénéficier d'un iδ = 1 on va incliner le massif de manière à ce que la résultante des efforts dans les butons s'applique verticalement. En pondérant l'inclinaison des butons par l'intensité des charges, on trouve une inclinaison du massif de 27.70°. On fixe maintenant la distance d = 0.50 mètre correspondant à la distance entre la base du massif et la surface en fond de fouille. Par itérations on trouve iβ = 0.86 et les dimensions suivantes du massif : 1.20 x 1.20 mètre :

En considérant maintenant le diamètre b = 0.20 mètre des butons, la dimension B = 1.20 mètre du massif, il vient une épaisseur minimale de 0.26 mètre pour garantir sa rigidité ( (B-b)/4 < d < (B-b))...et avec des aciers fy = 500 MPa et Ys = 1.15 on trouve une section d'acier minimale de 6.78 cm² par sens (soit 2 x 6HA12) :

ETAPE 3 : DETERMINATION DES EFFORTS DANS LE VOILE

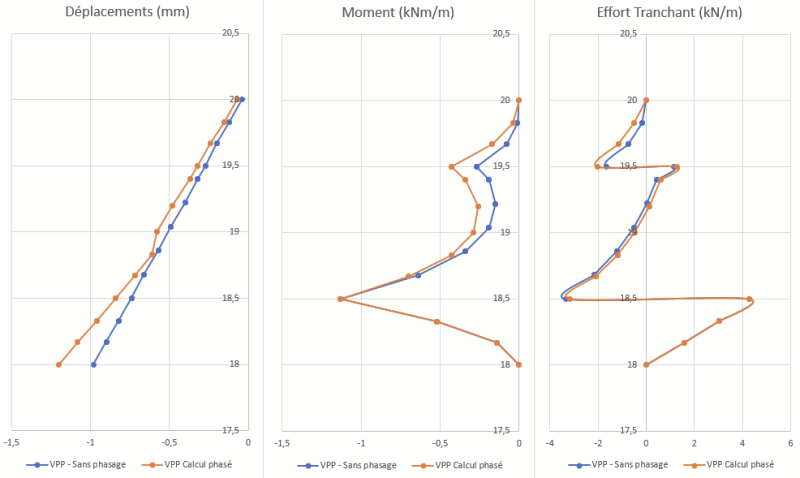
Ce site étant principalement fréquenté par des structuralistes je ne vais pas ici commettre l'affront de détailler le calcul des courbes de moments et d'efforts tranchants dans le voile. A partir des équations de la statique, tranche par tranche, ici selon un pas de 5 cm, on obtient facilement les courbes suivantes :

Il ne reste plus au structuraliste qu'à dimensionner les armatures du voile au niveau de la travée, au niveau des appuis et des bandes noyées ()

CONCLUSIONS ET REMARQUES COMPLEMENTAIRES

L'utilisation de l'utilitaire "KaMEL" permet donc de faire rapidement un pré-dimensionnement d'un voile par passes, butonné, cependant, en phase EXE vous devrez nécessairement passer par un calcul MISS.

Pour infos, la comparaison des résultats obtenus avec KREA (calcul MISS) et KaMEL (calcul MEL) pour l'exemple développé précédemment montre les différences suivantes :

On remarque des rapports de l'ordre de 5 à 9% pour l'ensemble des valeurs sauf pour le moment min ou le ratio est beaucoup plus élevé au niveau du "ventre mou" de la paroi.

Au final, cette méthode analytique reste acceptable en avant-projet notamment pour l'estimation des réactions au niveau des butons et des efforts de cisaillement. Par contre, il est nécessaire d'appliquer une majoration aux moments pour rester dans des ordres de grandeurs proches de ceux obtenus avec la méthode MISS. A priori un coefficient de majoration de 1.20 appliqué aux moments peut permettre de compenser ces écarts.

Voilà, voilà, bon dimanche.

Bien à vous

 

Bonjour @CHARIH,

La raison est simplement géométrique ; lorsque le premier bandeau est réalisé, les passes du second bandeau ne peuvent être faites qu'entre les butons retenant le premier bandeau :

On a donc pas le choix, les passes du bandeau inférieur seront donc nécessairement décalées par rapport à celles du bandeau supérieur.

Cordialement

Quid des déplacements créés par les VPP ?

Bonsoir @CHARIH,

Oui effectivement c'est bien là la limite de cette approche MEL (Méthode d'Equilibre Limite) et des équations de la statique en général. Cette approche ne tiens pas compte des rigidités propres des éléments structuraux. Par conséquent, elle ne permet pas d'évaluer les déplacements et déformations des éléments.

C'est bien pour cela qu'au début du sujet j'insiste fortement sur le fait que cette approche "simple" et "rapide" ne doit être utilisée qu'en phase AVP ou en prédimensionnement.

En phases PRO ou EXE, il faut passer sur une méthode MISS (Méthode d'Interaction Sol Structure) plus complète, basée sur :

• l'équation générale des poutres, tenant compte des produits E.I. des éléments structuraux,
• les modules de réaction horizontale du sol.

Pour cela on peut faire appel à des logiciels spécialisés type RIDO ou KREA.

(NOTE : une application basée sur ces mêmes principes est en cours de développement. Je n'avance pas aussi vite que je veux mais dès qu'elle sera prête je pourrais la rendre disponible à tous sur mon site )

Cordialement

@CHARIH, je me permet d'ajouter que même à partir des données issues de l'analyse présentée dans mon post, on peut quand même tenter d'approcher les déplacements en considérant les appuis (les butons) avec une rigidité infinie et en utilisant des "Formulaires des poutres" que l'on peut trouver facilement sur Internet. Ces formulaires permettent de calculer facilement, en fonction des efforts et du produit E.I. du voile, la flèche entre 2 appuis et la flèche en porte-à-faux. Si on ajoute le raccourcissement élastique des butons et le déplacement (tassement) de la semelle, alors, avec un peu de géométrie, on peut obtenir des valeurs approchées assez réalistes des déformées et des déplacements au niveau du voile.

J'ai fait l'expérience avec l'exemple que je présente au début du sujet et comparé les résultats avec un calcul sous KREA...c'est plutôt pas mal (avec des différences de l'ordre de 5 à 10 % sur le modèle testé).

Je ne connais pas bien les logiciels de structure mais il me semble qu'avec un logiciel comme PyBar (téléchargeable gratuitement) on peut aussi obtenir une approche réaliste des déformées en considérant simplement l'inertie de la poutre (le voile) posée sur 2 appuis et les efforts appliqués.

Voilà, voilà,...les équations de la statique et la méthode MEL ne permettront jamais d'atteindre la précision et la souplesse d'une approche MISS, mais, en avant projet...ou en prédimensionnement...bref...en première approche, elles ont l'avantage de donner rapidement et facilement des résultats suffisamment fiables pour juger de la faisabilité ou non de la solution et pour réaliser un chiffrage dans le cadre d'une réponse à un appel d'offre.

PS : ceci étant dit, vous m'avez convaincu...et je vais essayer d'implanter une approche des déplacements dans mon application KaMEL ...je vous ferai savoir lorsque ce sera disponible en ligne.

Bien cordialement

Merci vos interventions inédites.

Vous avez dit que vous avez utilisé Krea pour le calcul des VPP .

A ma connaissance ce logiciel ne les couvre pas.

Aussi si nous avons une structure fragile qui ne tolère  disons pas  plus de 5 mm de déplacements.

Pensez vous que pour ce cas cette solution reste valable.

Bonjour @CHARIH,

Je vous confirme que OUI le logiciel KREA permet bien de dimensionner des voiles par passes...il suffit juste d'adapter le modèle aux différentes étapes. La preuve ci-dessous en tenant compte de l'exemple développé au début de ce post :

On retrouve sur les graphes ci-dessus les mêmes valeurs de moments et d'efforts tranchants que ceux calculés précédemment.

Pour votre cas d'étude, le fait de savoir si cette solution reste acceptable ou pas en termes de déplacements nécessite justement de recourir à une méthode MISS.

Je ne connais pas les caractéristiques de votre cas d'étude, mais, si on reprend l'exemple que j'ai développé au début de ce post, les déplacements sont de l'ordre de 2 millimètres en tête.

Donc en résumé :

• pour un dossier classique sans exigence particulière notamment sur les déplacements, les équations de la statiques et la méthode MEL (et mon application KaMEL) permettent de faire simplement et rapidement, avec une précision suffisante, un prédimensionnement correcte au stade AVP,
• pour un dossier avec des exigences particulières (en termes de déplacements par exemple), ou dans le cas d'un dimensionnement PRO/EXE, alors on doit passer par la méthode MISS (avec par exemple KREA ou RIDO).

 

Cordialement

Je vous ai posé cette question car dans les tutoriels ça ne traite pas des VPP.

Merci.

@CHARIH y'a pas de soucis, effectivement ces sujets ne sont pas traités dans le manuel KREA. Le logiciel est normalement destinées aux parois, butonnées/tirantées ou non, et généralement ancrées. Mais avec un peu de pratique, on peut tout à fait traiter le cas des voiles non ancrés.

J'essaierai ce WE de compléter ce sujet en détaillant les étapes de calcul d'une évaluation "simple" des déplacements.

Cordialement

Merci.

Trois nouvelles questions me sont venues à l'esprit :

La première sur les aciers en attente.

La deuxième si les butons peuvent être réalisés de manière horizontale.

Je vois qu'en France on utilise beaucoup des butons en bois.

Bonsoir @CHARIH,

• pour les aciers en attente ? Quelle est la question ?  => je ne suis pas structuraliste donc pas sûr de pouvoir vous répondre.
• les butons peuvent 'ils être horizontaux ? => oui, si la fouille est étroite alors les butons peuvent être horizontaux appuyés de chaque coté sur les voiles contre terre
• En France on utilise beaucoup des butons en bois => oui c'est vrai mais pour des fouilles assez modestes. La production de butons en bois respecte des critères de sélection des bois (présence de nœuds, ...etc...) qui permettent de "garantir" certaines caractéristiques intrinsèques (notamment le module d'Young du bois). On peut donc tout à fait intégrer cela dans un calcul. Si les sollicitations sont encaissables par le buton bois alors rien ne s'oppose à son utilisation sur chantier.

Cordialement