- Réponses 3
- Vues 1.7k
- Créé
- Dernière réponse
Meilleurs contributeurs dans ce sujet
-
 Wheatley 2 messages
Wheatley 2 messages -
alex beebire 1 message
Jours populaires
Messages populaires
-
Bonjour, Comme simple aide je peux vous orienter ainsi : 1/ Tout d'abord je suppose que vous avez déterminé quel point X est le repère de calcul de tes moments, si non il faut le fai




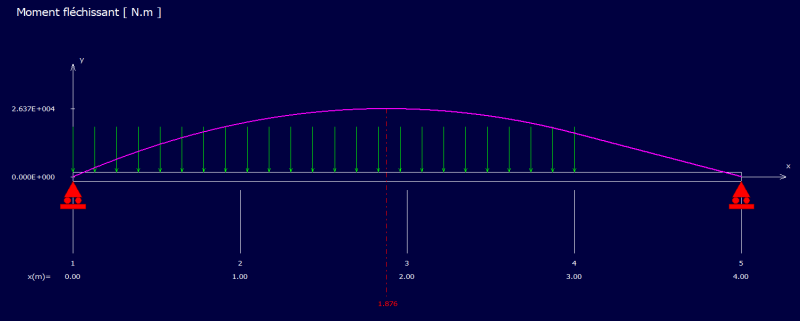
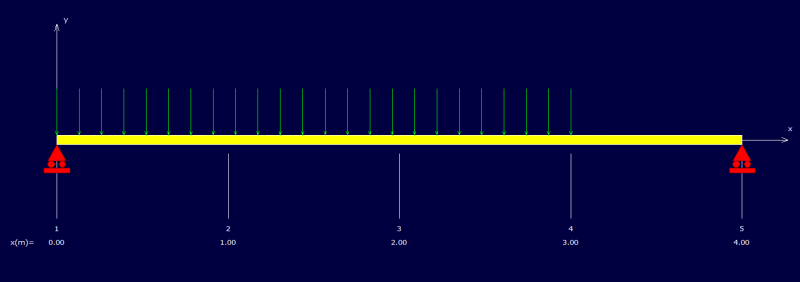
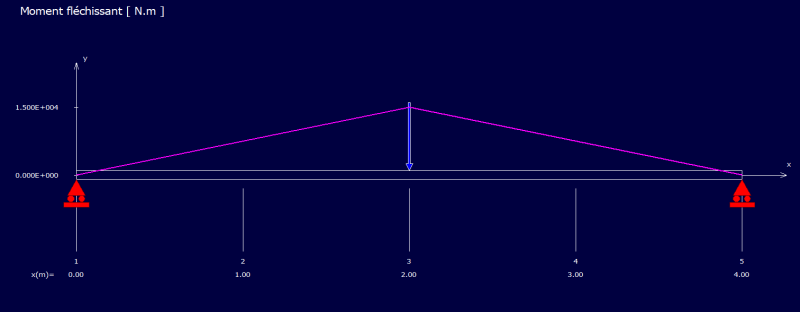
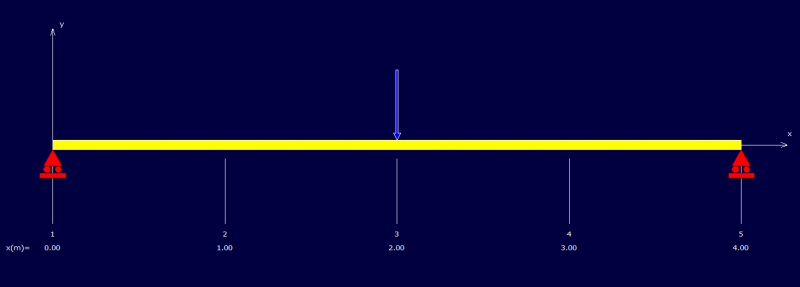
comment_147964Bonjour,
J'essaye de me faire un fichier Excel permettant de trouver l'emplacement du moment pondéré Max ainsi que sa valeur.
J'ai une poutre de longueur L sur appuis simple avec une charge distribué permanente et libre sur toute la longueur et un nombre quelconque de charges ponctuelles permanente et libres ( les charges ponctuelles permanentes et libres ont le meme emplacement mais peuvent avoir des valeurs differentes, ex si Pd1=20Kn a 2m alors Pl1 peut avoir n'importe quelle valeur mais doit etre a 2m.
J'essaye donc de trouver une formulation general qui marchera pour n'importe quelles valeurs de Wd, Wl, Pdi et Pli.
J'ai trouve les reactions d'appuis qui sont de (SommePixi + Wd.L^2 / 2 ) 1/L, mais apres les charges ponctuelles me derangent pour trouver une formulation generale.
C'est pourquoi j'ai besoin que l'on me debloque.
Merci d'avance