- Replies 19
- Views 3.7k
- Created
- Last Reply
Top Posters In This Topic
-
ingAddict 9 posts
-
 KARIMTCA 4 posts
KARIMTCA 4 posts -
Tony_Contest 3 posts
-
 Bisudi Bazola Aimé 2 posts
Bisudi Bazola Aimé 2 posts
Most Popular Posts
-
Bonjours, D’une manière qualitative (sans aucun calcul) la tête du poteau dans la direction de l’axe Z est connecté ‘’monolithiquement’’ à un plancher (nervuré selon la figure) et à deux poutres
-
Bonjour, Le poteau est tenu en tête dans toutes les direction (plancher coulé et 3 poutres en liaison). En le considérant articulé, ce qui est le cas le plus courant, sa hauteur de flambemen
-
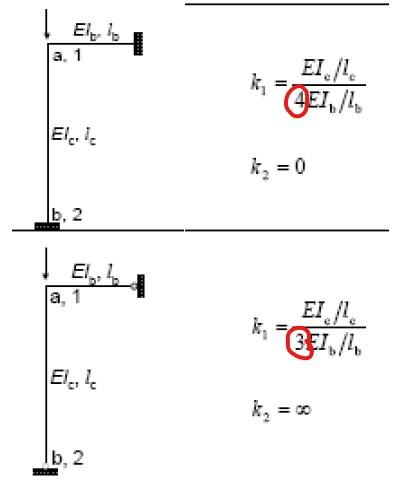
Bonjour , Je pense qu'on peut prendre un coefficient proche de 0,7. Mais je remarque que le taux de travail 83 % (1/1,2 = 0,83) est comme même grand, pourquoi ne pas élargir la colonne ainsi tu




.png.4934dd780339f8f4aeb0d1144fe6e598.png)
comment_151369bonjour à tous,
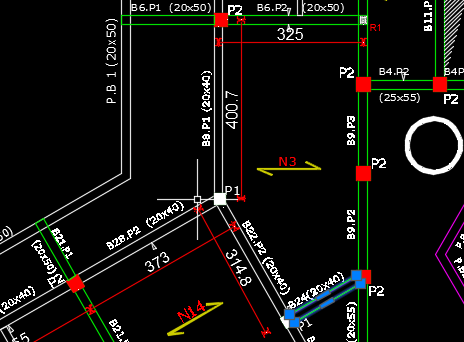
étant chargé de vérifier le poteau P1 ci dessus,
ma question est comment déterminer le coefficient de flambement du poteau dans l'axe Z si on considère l'axe Y parallèle à B8.
P1 (25x25, hauteur 4m, charge ELU 600KN, nœuds non déplaçable).
Merci.