- Réponses 64
- Vues 11k
- Créé
- Dernière réponse
Meilleurs contributeurs dans ce sujet
-
BELLAMINE 36 messages
-
Tony_Contest 18 messages
-
 KARIMTCA 3 messages
KARIMTCA 3 messages -
FRIDJALI 3 messages
Jours populaires
Messages populaires
-
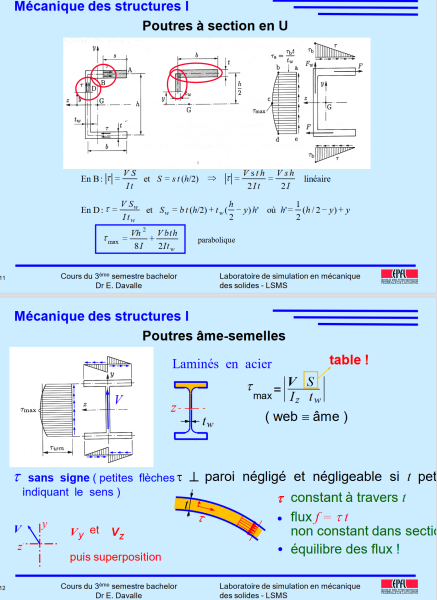
Bonjour, C'est bien ça. L'effort rasant causant le cisaillement des boulons est bel et bien due à l'effort tranchant. Je vous renvoie vers la littérature (effort rasant en charpente métallique. )
-
Bonjour, L'effort rasant, vaut à l'interface : V SUPE200/Axe neutre/Iglobal UPE200+IPE270 Effort par unité de longueur (N/ml par exemple si V est en N) Attention, S est le moment stati
-
bonjour partage moi ton probleme en email je suis connecte de mobile image non accessible cordialement





comment_154684Bonjour,
Je ne sais pas si le sujet a été traité ou pas. Si c'est le cas, pouvez vous me rediriger vers le sujet sinon j'en appelle à votre savoir .
.
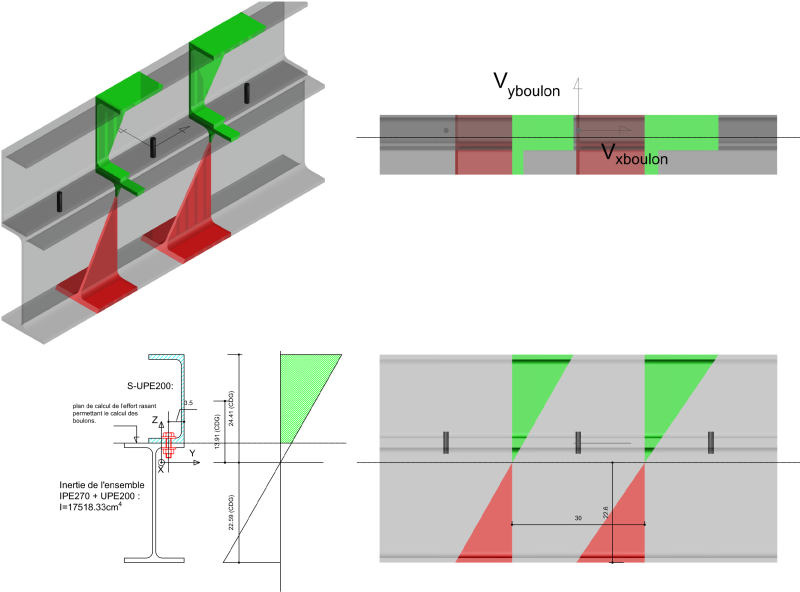
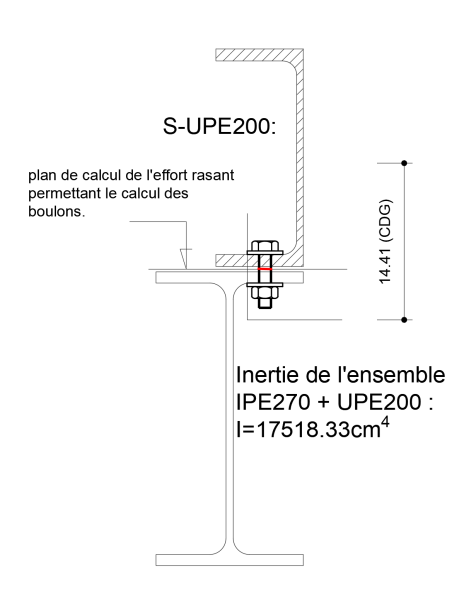
En pièce jointe, vous trouverez la vue en coupe des pièces que je souhaiterais assembler. À la base dans le projet n'était prévu que l'IPE 270, pour des raisons esthétiques on doit préserver celui-ci est rajouter un UPE par dessus pour le renforcer.
Ma problématique : justifier tout cela aux ELU…
Il faut prendre comme hypothèse qu'une charge répartie est appliquée tout le long et qu'une charge ponctuelle pourrait être appliquée en un point (1,3m du bord), longueur de poutre 11,9m.
Je veux donc vérifier aux ELU la contrainte dans chacun des profilés. je veux aussi déterminer quelle est la valeur du cisaillement à prendre en compte dans le boulonnage... Ou plutôt pour une résistance de boulons donnée, combien il faut en mettre en œuvre…
Il faudra peut-être aussi modifier le sens de l'UPE pour que les âmes soient alignées entre les deux profilés...