- Réponses 12
- Vues 3.4k
- Créé
- Dernière réponse
Meilleurs contributeurs dans ce sujet
-
Zied1 5 messages
-
FRIDJALI 3 messages
-
BELLAMINE 3 messages
-
Tony_Contest 1 message
Jours populaires
Messages populaires
-
Bonjour Le moment dû à l'excentricité e au centre de gravité de la semelle vaut M=+pu.e celui qui équilibre M dans le mur vaut M'=-M. Donc au centre de gravité de la semelle on a un moment M" = M
-
bonjour, il n'est pas précisé de quel type de mur il s'agit. Pa ailleurs d'o* viendrait le moment qui équilibrerait le moment du à l'excentricité? A+
-
re-bonjour, Désolé, mais les trois derniers posts ne m'ont apparu qu'après ma question. d'un autre coté, les les extrait donnés par @Zied1ne sont pas très exploitables car e sont des bribes




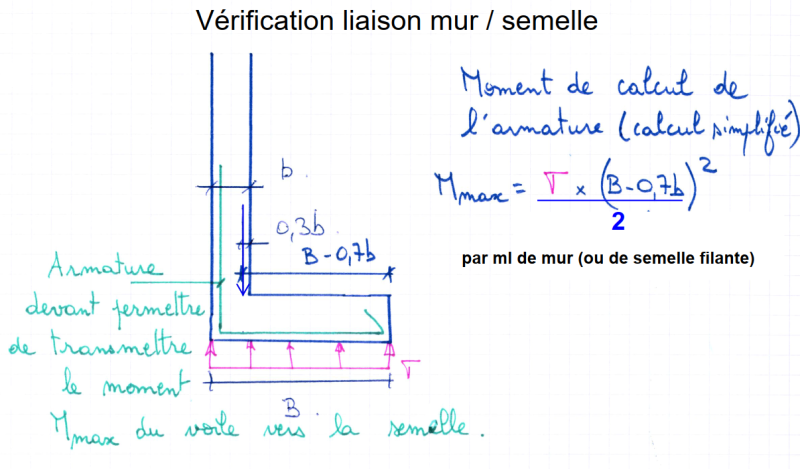
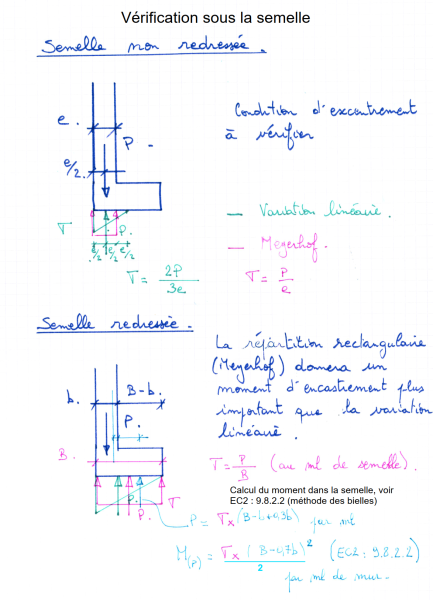

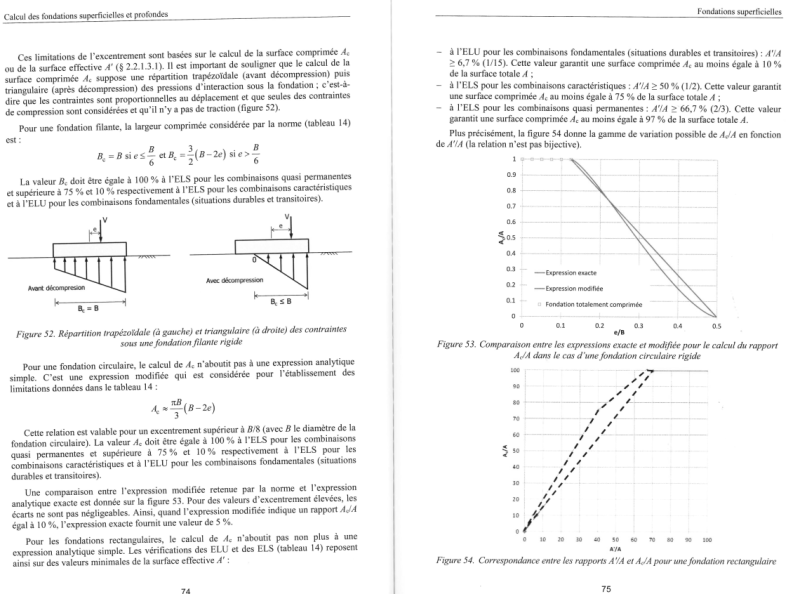
comment_205287Bonjour à tous,
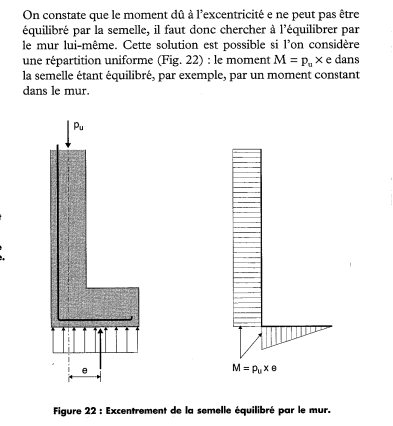
Je souhaite discuter d'un sujet très intéressant dans le domaine des structures, et plus spécifiquement dans le domaine des fondations des bâtiments : la semelle excentrée.
Pour parvenir à l'équilibre de la semelle, plusieurs méthodes sont utilisées, telles que :
1-Une répartition linéaire des réactions du sol suivant un diagramme triangulaire ou trapézoïdal.
2- Un couple obtenu par une force de frottement à l'interface sol-semelle et une autre force horizontale au niveau du plancher.
3-Un couple obtenu par une force au niveau du dallage et une autre force horizontale au niveau du plancher.
4-La flexion du mur.
5-Des longrines de redressement.
Je souhaite poser une question concernant l'équilibre par le mur : Est-ce qu'avec cette méthode, le diagramme de contrainte sous la semelle est rectangulaire ? Et peut-on travailler comme s'il s'agissait d'une semelle centrée ? Est-ce que l'on élimine la vérification supplémentaire de l'équilibre de la semelle et vérifie seulement la contrainte admissible ? (Bien sûr, à condition que le ferraillage de la semelle soit correct, avec un moment identique à la fois dans la semelle et dans le mur) (une photo ci dessous traduit ma situation)
Je vous prie de m'excuser si ma question n'est pas claire et je vous remercie par avance pour votre aide.