- Réponses 22
- Vues 5.1k
- Créé
- Dernière réponse
Meilleurs contributeurs dans ce sujet
-
 Issamania 7 messages
Issamania 7 messages -
Tony_Contest 5 messages
-
 Bisudi Bazola Aimé 4 messages
Bisudi Bazola Aimé 4 messages -
Zied1 3 messages
Jours populaires
Messages populaires
-
Bonjour je te donne le principe , et pour les calculs le BET peuvent le faire pour toi ou toi meme tu peux le faire .le retrait et la temperature provoque une augmentation de la cont
-
Bonjour, Le projet concernant un bassin, le gradient thermique est l'écart de plus défavorable entre une face et la face opposée du bassin. Par exemple : température du liquide dans le bassi
-
Lambda b pour celui du béton, le lambda précédent est celui qui correspond au schémas de la norme (vous avez pris la norme de 1998). Si le mur est en béton, c'est également celui du béton. Le f




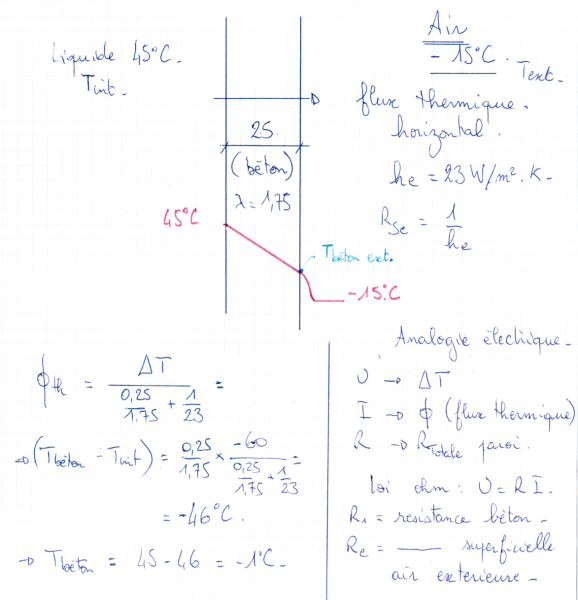
comment_206706Bonjour tous le monde,
Je viens vers vous pour éclairer ma lanterne, j'ai un voile de 55 m de longueur à Chlef et je ne peux pas faire un joint,comme j'ai jamais fait ça merci de m'orienter sur le calcul du gradient thermique car je ne trouve aucune formule dans le CBA93,merci.