- Réponses 12
- Vues 1.5k
- Créé
- Dernière réponse
Meilleurs contributeurs dans ce sujet
-
BELLAMINE 9 messages
-
Tony_Contest 3 messages
Jours populaires
Messages populaires
-
Bonjour, Equilibre des moments ne donne qu'une seule équation, que vous le fassiez en A ou en B c'est la même équation. Le système a donc 3 équations (somme des force selon X=0, somme des fo
-
Bonjour, La somme des moments (par rapport à Z), cela ne fait qu'une équation, vous pouvez faire le calcul en A, en B ou en n'importe quel point. Ici, il n'y a que 3 équations fondamentales




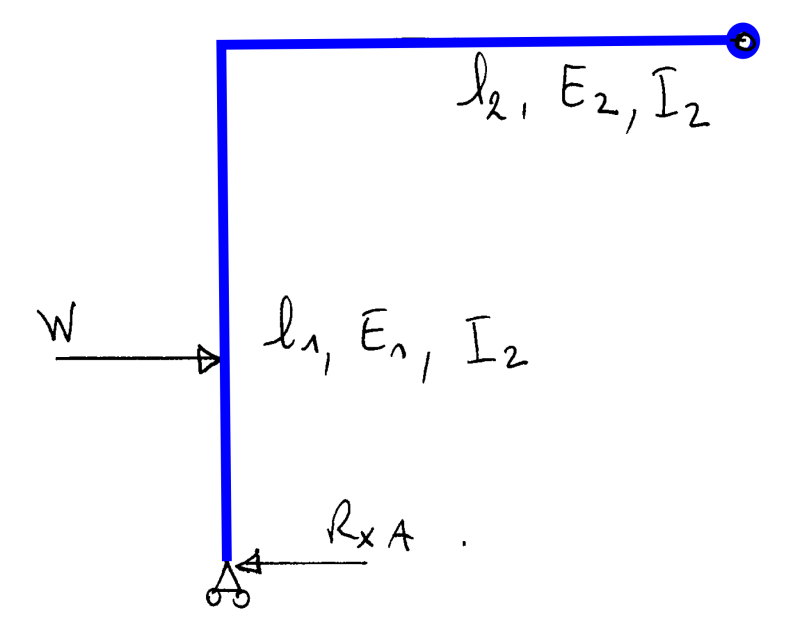
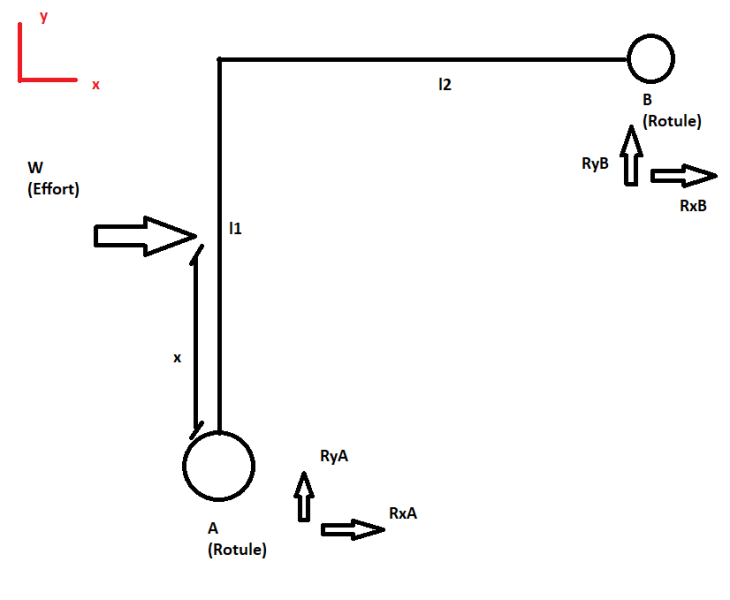
comment_219782Bonjour,
Je suis entrain d'étudier une structure, et j'étais bloqué lors l'extraction des reactions. Pouver vous s'il vous plais m'aider pour trouver ces reactions?
Le système est clairement hyperstatique, du coup je me galère...
Ci-joint un Sketch
Merci