- Réponses 28
- Vues 34.3k
- Créé
- Dernière réponse
Meilleurs contributeurs dans ce sujet
-
Richesse d'Esprit 5 messages
-
FRIDJALI 3 messages
-
Lionnet 3 messages
-
 Ahmed أحمد 2 messages
Ahmed أحمد 2 messages
Jours populaires
Messages populaires
-
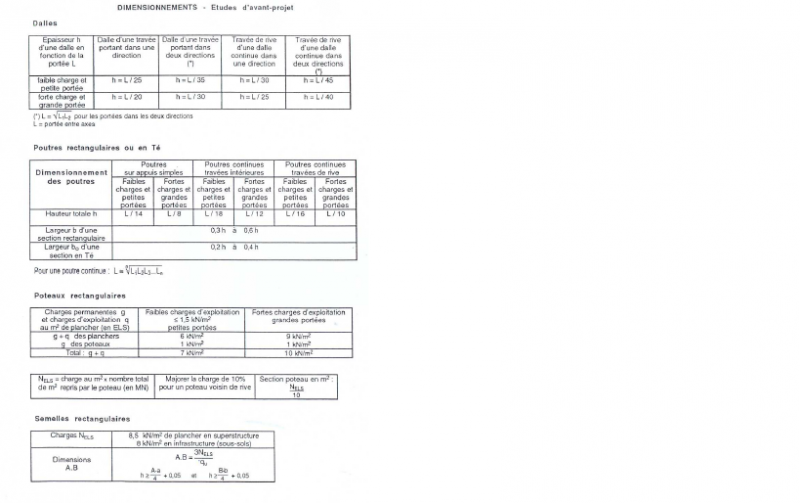
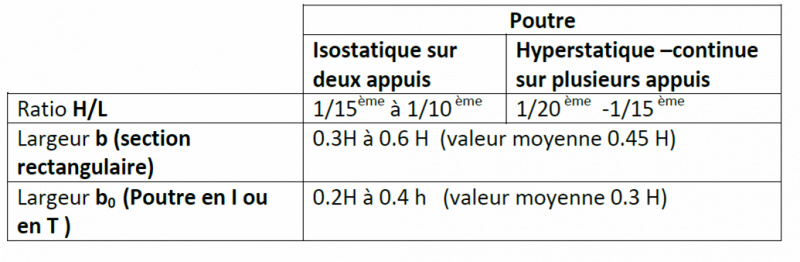
Poutre : En cas d'une poutre isostatique : L/10 : L étant la portée entre axe de poteaux En cas d'une poutre hyperstatique( à plusieurs travées) : L/16 Poteau : S (m²) étant la section d'un
-
bonjour, j'ajoute à ce qui a été que ces règles n'ont pas un cadre normatif mais comme leur nom l'indique ce sont des règles de pré dimensionnement qui permettent de faire la descente de charge. Mais
-
salam ; pour les poutres porteuse c'est L /12.5 pour les poutres non porteuse c'est L/16 suit à L= la porté de la poutre bonne chance







comment_39279slt tt le monde, je cherche les règles de prédimensionnement des structures en béton armé (poteau, poutres, plancher...)